This document is an SR study of reference frame transformations as applied to a “Square in a Rectangle”. It is the way I do it in my computer program. If you are interested, it goes like this.

1. Initial Conditions:

Start with a referenced frame for which a Square (2 light seconds on each side) is at rest at the origin at time t = 0. There is a Rectangle (really just a larger square 2.2 light seconds on each side) coincident with the square but it has a velocity of (vx, vy) = (-.6c, 0) with respect to the reference frame. There is also a third observer whose velocity is (-.6c, .6c), location not important.

The 4 corners of the Square would have space-time coordinates of;

Square_a (t, x, y) = (0, +1, +1)

Square_b (t, x, y) = (0, -1, -1)

Square_c (t, x, y) = (0, +1, -1)

Square_d (t, x, y) = (0, -1, +1)

The 4 corners of the “Rectangle” would have contracted space-time coordinates of;

Rect_a (t, x, y) = (0, +1.1, +1.1)

Rect _b (t, x, y) = (0, -1.1, -1.1)

Rect _c (t, x, y) = (0, +1.1, -1.1)

Rect _d (t, x, y) = (0, -1.1, +1.1)

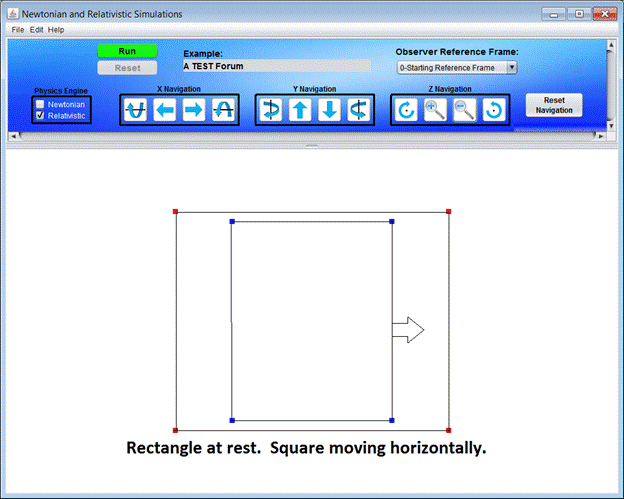
See Picture below:

The issue is that no matter how many reference frame transformations, the Square will always fit in the “Rectangle”. So here are 2.

2. Transform both sets of corners to a reference frame for which the rectangle is at rest. You already know this will result in the “Rectangle” losing its width contraction and the Square acquiring some. But the calculation makes for a good warm up. Set up the Lorentz Transform with vx = -.6c and use it to transform each corner.

Square_a (t, x, y) = (0, +1, +1) transforms to --> (+.75, +1.25, +1)

Square_b (t, x, y) = (0, -1, -1) transforms to --> (-.75, -1.25, -1)

Square_c (t, x, y) = (0, +1, -1) transforms to --> (+.75, +1.25, -1)

Square_d (t, x, y) = (0, -1, +1) transforms to --> (-.75, -1.25, +1)

Rect_a (t, x, y) = (0, +1.1, +1.1) transforms to --> (+.825, +1.375, +1.1)

Rect _b (t, x, y) = (0, -1.1, -1.1) transforms to --> (-.825, -1.375, -1.1)

Rect _c (t, x, y) = (0, +1.1, -1.1) transforms to --> (+.825, +1.375, -1.1)

Rect _d (t, x, y) = (0, -1.1, +1.1) transforms to --> (-.825, -1.375, +1.1)

Now take Relativity of Simultaneity (RoS) into account. Recognize that, with respect to the new reference frame, the “Square” and all its corners are moving at vx = +.6c. So, if corner “A” is at (x, y) = (1.25, 1) at time t’ = .75 sec, where was it at t’ = 0? Well, in .75 sec the corner moved .75 *.6c = .45 light-sec. So, subtract out the amount it moved +1.25 – (.75*.6) = 1.25 -.45 = .8 to get its space coordinates at t’ = 0. Repeat for all corners of the Square.

Square_a (t’, x’, y’) = (+.75, +1.25, +1) -- RoS --> (0, +.8, +1)

Square_b (t’, x’, y’) = (-.75, -1.25, -1) -- RoS --> (0, -.8, -1)

Square_c (t’, x’, y’) = (+.75, +1.25, -1) -- RoS --> (0, +.8, -1)

Square_a (t’, x’, y’) = (-.75, -1.25, +1) -- RoS --> (0, -.8, +1)

Note that I chose to determine all the space coordinates for the common time t’ = 0 with respect to the new reference frame. I could have chosen any time but zero makes it easy to recognize the resulting shape. Width is contracted as expected (20%).

You can apply same logic to “Rectangle” coordinates or just recognize that since the “Rectangle” is at rest with respect to this reference frame the x and y coordinates will never change.

Rect_a (t’, x’, y’) = (0, +1.375, +1.1)

Rect _b (t’, x’, y’) = (0, -1.375, -1.1)

Rect _c (t’, x’, y’) = (0, +1.375, -1.1)

Rect _d (t’, x’, y’) = (0, -1.375, +1.1)

See picture below.

3. Now transform the shapes from step 2 to a reference frame where the third observer is at rest. First, what is the relative velocity of the third observer with respect to the reference frame of the “Rectangle”? It is NOT (vx, vy) = (0, .6c).

Relativistic Velocity Composition (-.6c, +.6c) - (-.6c, 0) = (0, .75c).

So set up the Lorentz Transformation with (vx, vy) = (0, .75c) and use it to transform each corner. You need the full 3D transform for this.

Square_a (t’, x’, y’) = (0, +.8, +1) transforms to --> (-1.134, +.8, +1.512)

Square_b (t’, x’, y’) = (0, -.8, -1) transforms to --> (+1.134, +.8, -1.512)

Square_c (t’, x’, y’) = (0, +.8, -1) transforms to --> (+1.134, +.8, -1.512)

Square_d (t’, x’, y’) = (0, -.8, +1) transforms to --> (-1.134, +.8, +1.512)

Rect_a (t’, x’, y’) = (0, +1.375, +1.1) transforms to --> (-1.247, +1.375, +1.663)

Rect_b (t’, x’, y’) = (0, -1.375, -1.1) transforms to --> (+1. 247, -1.375, -1.663)

Rect_c (t’, x’, y’) = (0, +1.375, -1.1) transforms to --> (+1. 247, +1.375, -1.663)

Rect_d (t’, x’, y’) = (0, -1.375, +1.1) transforms to --> (-1. 247, -1.375, +1.663)

Again take Relativity of Simultaneity into account. The velocity of the Square in the new reference frame is (vx, vy) = (.396, -.75). Now consider corner “A” again. If corner “A” is at (x, y) = (.8, 1.512) at time t’’ = -1.134 sec, where will it be at t’’ = 0? Add in the amount it will move (.8, 1.512) + (1.134*.396, 1.134*-.75) = (1.25, .661) to get its space coordinates at t’’ = 0. Repeat for all corners of the Square.

Square_a (t’’, x’’, y’’) = (-1.134, +.8, +1.512) -- RoS --> (0, +1.25, +.661)

Square_b (t’’, x’’, y’’) = (+1.333, -.6, -1.666) -- RoS --> (0, -1.25, -.661)

Square_c (t’’, x’’, y’’) = (+1.333, +.6, -1.666) -- RoS --> (0, +.35, -.661)

Square_d (t’’, x’’, y’’) = (-1.333, -.6, +1.666) -- RoS --> (0, -.35, +.661)

Again take Relativity of Simultaneity into account. The velocity of the “Rectangle” in the new reference frame is (vx, vy) = (0, -.75). Now consider corner “A” again. If corner “A” is at (x, y) = (+1.375, 1.663) at time t’’ = -1.247 sec, where will it be at t’’ = 0? Add in the amount it will move (+1.375, 1.663) + (1. 247 *.0, 1. 247 *-.75) = (1.375, .727) to get its space coordinates at t’’ = 0. Repeat for all corners of the “Rectangle”.

Rect _a (t’’, x’’, y’’) = (-1.247, +1.375, +1.663) -- RoS --> (0, +1.375, +.727)

Rect _b (t’’, x’’, y’’) = (+1.247, -1.375, +1.663) -- RoS --> (0, -1.375, -.727)

Rect _c (t’’, x’’, y’’) = (+1.247, +1.375, +1.663) -- RoS --> (0, +1.375, -.727)

Rect _d (t’’, x’’, y’’) = (-1.247, -1.375, +1.663) -- RoS --> (0, -1.375, +.727)

See picture below.

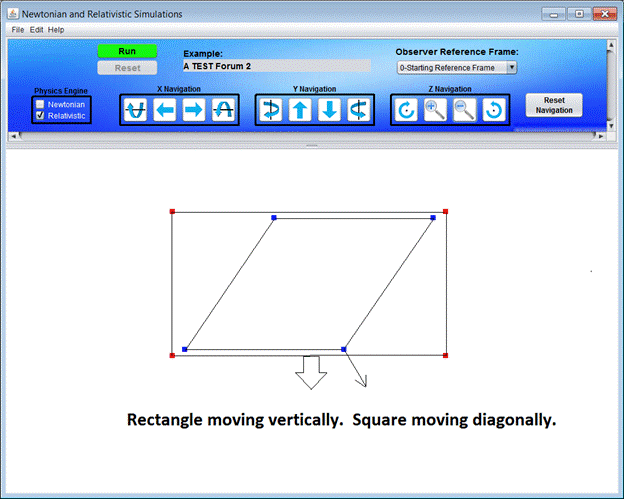
Summary:

Very important to recognize the shape of the “Square” after the second transformation. It is contracted both vertically and diagonally. It is not a square contraction in the direction of relative motion.